It’s More Probable Than You Think

from - MARTIN GARDNER

Three hundred years ago, a gambler asked Blaise Pascal, the French mathematician, how to calculate the odds on certain dice throws. Pascal’s answers were the beginning of “probability theory,” now one of the fastest-growing branches of mathematics. Physicists use it to compute the probable path of a neutron through heavy water, geneticists to determine the likelihood that a couple will have blue-eyed children. Businessmen, economists, politicians, military leaders - it is hard to think of a profession in which probability theory is not applicable.

In daily life we make countless decisions based on intuitive, common-sense estimates of probability; most of the time these estimates are fairly reliable. Yet experts have found all sorts of curious situations in which the actual probabilities differ startlingly from what we expect.

One of the most difficult of all probability calculations to believe is what mathematicians call the birthday paradox. Say that you are attending a party at which 23 people are present. What is the probability that two of you were born on the same day of the same month? Intuitively, you feel that the probability is low. Actually, the chances are about even.
One way to work this out: Take any two people, and the chances are 364 out of 365 - or, there is a 364/365 probability - that their birth dates won’t match. The chance that a third person’s birth date will miss both of theirs is 363/365; a fourth person’s 362/365; and so on. Then, since the probability that all of a series of separate events will occur (meaning, in this case, that all the birthdays will be different) is the product of the probabilities for each individual event, you multiply all these fractions together. As it turns out, by the time you have 23 people in the series, the probability fills below half; in other words, it becomes a trifle better than even chance that, out of 23 birth dates, two will coincide.
With more people, the probability of a match goes up rapidly. For 30 people, the probability is better than 7/10, or odds of 7 to 3 in favour of two coinciding dates. With 50 people, the chances are better than 97 out of 100!
This seems so contrary to common sense that you may want to test it when you are at a gathering of 23 or more people. Or go through a Who’s Who and check 30 names at random. Seven times out of ten you’ll find a pair of matching birth dates.

Professional gamblers know all sorts of “sucker bets” based on the same principle as the birthday paradox. A gambler will bet you at even odds, for example, that of the number plates on the next 20 passing cars, at least two will match each other in their last two numerals. It sounds like a good bet? The odds actually are 7 to 1 in his favour.To work out the probability of any one outcome, you need to know the number of different, equally possible outcomes. When you toss a coin there are just two possibilities - heads or tails - so the probability of flipping either is 1/2. In less simple situations, however, it is easy to overlook some of the possible outcomes and so arrive at a false probability estimate.

For example: What is the probability that, if a family has three children, they will all be of the same sex? One might reason: “At least two of the children are certain to be of the same sex. The third, then, will either match them or it won’t - so the probability that all three will be alike must be 1/2.” But consider all the possible combinations, letting B stand for boy, G for girl: BBB, BBG, BGB, BGG, GBB, GBG, GGB, and GGG. Only two of those eight sequences - BBB and GGG - are all alike. The correct probability, therefore, that the three children will be of the same sex is 2/8, or 1/4.

Suppose a couple plans to have four offspring. Which is more likely: three children of one sex and one of the other, or two boys and two girls? Most people guess two and two. But when we list all the possible combinations - there are 16 - we see that in six cases there is a two-two split, but that there are eight sequences with a three-one split. So the probability is 1/2 that the sexes will be split three and one. Our intuition has played us false again!

Another way of going wrong when estimating probabilities is to assume that certain events are related when they are not. Many people imagine that if a coin comes up heads several times in a row, the odds will favour tails on the next toss. Not so. No matter how many times a coin lands heads up, the probability of heads on the next toss remains 1/2. Dozens of ridiculous systems for playing roulette and other games of chance are based on this “gamblers’ fallacy” that previous results have an effect on future results.

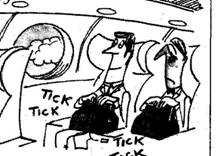Then there was the man who thought he could protect himself on plane trips by taking a harmless bomb along in his luggage (very unlikely these days). He reasoned that the odds against one person taking a bomb aboard were high, but that the odds against two people doing it were surely astronomical. His intuition was strong - but his grasp of statistics and probabilities was, to say the least, flawed. 

So the next time you’re hedging your bets, be brave... ~ SB